Ley de los gases ideales – deQuimica.com

La ley de los gases ideales es la apariencia negativa, un gas hipotético formado por partículas puntuales, sin atracción ni repulsión entre ellas y cuyos choques son perfectamente elásticos (conservación de momento y energía cinética). La energía cinética es directamente proporcional a la temperatura en un gas ideal. Los gases reales que más se aproximan al comportamiento del gas ideal son los gases monoatómicos en condiciones de baja presión y alta temperatura.

En 1648, el químico Jan Baptist van Helmont creó el vocablo gas, a partir del término griego kaos (desorden) para definir las génesis características del anhídrido carbónico. Esta denominación se extendió luego a todos los cuerpos gaseosos y se utiliza para designar uno de los estados de la materia.

La principal característica de los gases respecto de los sólidos y los líquidos, es que no pueden verse ni tocarse, pero también se encuentran compuestos de átomos y moléculas.

La causa de la naturaleza del gas se encuentra en sus moléculas, muy separadas unas de otras y con movimientos aleatorios entre si. Al igual que ocurre con los otros dos estados de la materia, el gas también puede transformarse (en líquido) si se somete a temperaturas muy bajas. A este proceso se le denomina condensación.

La mayoría de los gases necesitan temperaturas muy bajas para lograr condensarse. Por ejemplo, en el caso del oxígeno la temperatura necesaria es de -183°C.

Las primeras leyes de los gases fueron desarrollados desde finales del siglo XVII, aparentemente de manera independiente por August Krönig en 1856 1 y Rudolf Clausius en 1857. La constante universal de los gases se descubrió y se introdujo por primera vez en la ley de los gases ideales en lugar de un gran número de constantes de gases específicas descriptas por Dmitri Mendeleev en 1874.

En este siglo, los científicos empezaron a darse cuenta de que en las relaciones entre la presión, el volumen y la temperatura de una muestra de gas, en un sistema cerrado, se podría obtener una fórmula que sería válida para todos los gases. Estos se comportan de forma similar en una amplia variedad de condiciones debido a la buena aproximación que tienen las moléculas que se encuentran más separadas, y hoy en día la ecuación de estado para un gas ideal se deriva de la teoría cinética. Ahora las leyes anteriores de los gases se consideran como casos especiales de la ecuación del gas ideal, con una o más de las variables mantenidas constantes.

Empíricamente, se observan una serie de relaciones proporcionales entre la temperatura, la presión y el volumen que dan lugar a la ley de los gases ideales, deducida por primera vez por Émile Clapeyron en 1834 como una combinación de la ley de Boyle y la ley de Charles.

La ecuación de estado

El estado de una cantidad de gas se determina por su presión, volumen y temperatura. La forma moderna de la ecuación relaciona estos simplemente en dos formas principales. La temperatura utilizada en la ecuación de estado es una temperatura absoluta: en el sistema SI de unidades, kelvin, en el sistema imperial, grados Rankine.

La ecuación que describe normalmente la relación entre la presión, el volumen, la temperatura y la cantidad (en moles) de un gas ideal es:

$P \cdot V = n \cdot R \cdot T \,\!$

Donde:

P= Presion absoluta
V= Volumen
n= Moles de gas
R= Constante universal de los gases
T= Temperatura absoluta

Teoría cinética molecular

Esta teoría fue desarrollada por Ludwig Boltzmann y Maxwell. Nos indica las propiedades de un gas ideal a nivel molecular.

Todo gas ideal está formado por N pequeñas partículas puntuales (átomos o moléculas).
Las moléculas gaseosas se mueven a altas velocidades, en forma recta y desordenada.
Un gas ideal ejerce una presión continua sobre las paredes del recipiente que lo contiene, debido a los choques de las partículas con las paredes de este.
Los choques moleculares son perfectamente elásticos. No hay pérdida de energía cinética.
No se tienen en cuenta las interacciones de atracción y repulsión molecular.
La energía cinética media de la translación de una molécula es directamente proporcional a la temperatura absoluta del gas.

En estas circunstancias, la ecuación de los gases se encuentra teóricamente:

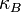$P V = N \kappa_{B} T \;$

Donde $\kappa_B$ es la constante de Boltzmann, donde N es el número de partículas.

La ecuación de estado para gases reales

Haciendo una corrección a la ecuación de estado de un gas ideal, es decir, tomando en cuenta las fuerzas intermoleculares y volúmenes intermoleculares finitos, se obtiene la ecuación para gases reales, también llamada ecuación de Van der Waals:

$\left ( P + \frac{a\cdot n^2}{V^2} \right ) \cdot (V - nb) = n \cdot R \cdot T$

Donde:

P= Presion del gas
V= Volumen del gas
n= Moles de gas
R= Constante universal de los gases ideales
T= Temperatura absoluta
a y b= son constantes determinadas por la naturaleza del gas con el fin de que haya la mayor congruencia posible entre la ecuación de los gases reales y el comportamiento observado experimentalmente.

Ecuación general de los gases ideales

Partiendo de la ecuación de estado:

$P \cdot V = n \cdot R \cdot T$

Tenemos que:

$\frac{P \cdot V }{n \cdot T} = R$

Donde R es la constante universal de los gases ideales, luego para dos estados del mismo gas, 1 y 2:

$\frac{P_1 \cdot V_1 }{n_1 \cdot T_1} = \frac{P_2 \cdot V_2 }{n_2 \cdot T_2} = R$

Para una misma masa gaseosa (por tanto, el número de moles «n» es constante), podemos afirmar que existe una constante directamente proporcional a la presión y volumen del gas, e inversamente proporcional a su temperatura.

$\left . \begin{array}{l} \cfrac{P_1 \cdot V_1}{T_1 \cdot n_1}=\cfrac{P_2 \cdot V_2}{T_2 \cdot n_2} \\ \; \\ n = \rm{Constante} \end{array} \right \} \longrightarrow \cfrac{P_1 \cdot V_1}{T_1} = \cfrac{P_2 \cdot V_2}{T_2}$